分数のわり算は、以下のように計算しますね。 4 ÷ 2 5 = 4 × 5 2 = 10 この式だけで説明しようとすると理解しにくいと思いますので、まずは簡単な無学年で分数に関する演習をする計算プリントです。 進級テストつき! 分数計算トレーニング (無学年) ・仮分数⇔帯分数 ・等しい分数 ・倍数/公倍数 ・約数/公約数 ・約分/通分 ・同分母たし算/引き算 ・分数のたし算/引き算 ・分数のかけ算 ・分数のわり算 ・10回のテスト形式で計算力を 分数の割り算を学び初めの頃は、今回のような理屈は、飲み込みづらいかもしれません。 まずは簡単なケースから計算してみると良いでしょう。 \ 2 \times \frac{1}{2}= 1\など、逆数の式をたくさん計算してみれば、ひっくり返して掛ける式も、自然と納得できるようになると思います。
分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
分数のわり算 6年生
分数のわり算 6年生-分母と分子に同じ数をかけても分数の値は変わらない ・・・2 3 = 2× 2 3× 2 = 4 6 = 2 3 2 3 = 2 × 2 3 × 2 = 4 6 = 2 3 実はこの2つを知っているだけで解決するのです。 1割り算は分数で表せる分数とは、ある数を 0 でない他の数で割った商を、横線の上(分子)に割られる数、横線の下(分母)に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。各項目では、加減乗除の四則計算について、それぞれの計算方法と簡単な計算例をご紹介してい




6年生 分数の割り算 まなび365 小学生の算数プリントを自動作成 無料で自宅学習
「分数÷整数」は、整数を分母にかけよう! 小学校の授業では、分数のわり算は「分数÷整数」から学びます。\(\frac{1}{3}\)÷2=\(\frac{1}{6}\) の ようなわり算です。このタイプのわり算は、最初のうちは、「整数を分母にかけましょう」と教わります。分数の割り算の解説 分数の割り算は、割るほうの分数の分子と分母を逆にして掛け算をおこなうことでできます。 約分が可能であれば約分までおこないましょう。 約分の電卓 1 2 ÷ 3 4 割り算(逆数 」という問題なら 6 ÷ 3 = 2 と計算して、1分で進む距離(分速)は「2km」と答が出せるでしょう *1
分数の割り算は、割る数を逆数にして掛けることで計算できます。 逆数とは、分数の分母と分子を入れ替えたもの です。 具体的に、「 分数÷分数 」の形と、「 分数÷整数 」の形について、それぞれの解き方を見ていきましょう。それでは、小数を分数に変換する方法を確認しておきましょう! とっても簡単なことですよ (^^) 考え方としてはこんな感じです。 03というのは3から小数点を左に1つ動かした数ですね。 つまり、3を10で割った数ということ。 そして、わり算を分数の形で分数のわり算 1 分数で割ることの意味と、真 分数÷真分数の計算の仕方を 考え、その計算ができる。 dl のペンキで㎡の板を塗るとき、こ のペンキ1dl で塗れる面積を求める式 を考える。 ・その式になる理由を考え、説明する。 ア-① (観察・ノート)
こんにちは、なぎさです。 分数のおさらい3回目。最終回です。 (1回目と2回目はこちらから。 分数のおさらい①、分数のおさらい②) 今回は、分数の掛け算、割り算と、分数の計算をちょっとだけ簡単にする方法、そして間違いやすい落とし穴について説明します。①分数の 割り算 1 〈本時〉 分数でわることの意味 を考える。 ・分数でわることの意味を数直線 をもとに考え説明する。 ・既習の計算や除法の 性質を想起させる。 評価① 真分数÷真分数の計算 の仕方を考える。 ・既習の分数を整数でわる除法の 3 割り算は2種類あるって知っていますか? まとめ 今回はあまり知られていない割り算「 「包含除(ほうがんじょ)」 」について解説しました。 納得しないと先に進めない子にとって、理由の説明もなく「分数の割り算は、逆数をかける」と言われると



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料



1
分数×分数 ≪逆数≫ 分数÷整数 分数÷分数 これを見てわかるように、大日本図書 は他の3社と異なり、分数と整数の乗除 をやってから、分数と分数の乗除を載せ ている。また大阪書籍は、逆数をかけ算 とわり算の間に入れ、分数のわり算で このペンキ1dLでは、何m²ぬれますか。 どんな式になりますか。 昨日の問題と同じで、1dLを求めている。 式は、 4 9 4 9 ÷ 2 3 2 3 です。 分数×分数の計算は、分子と分母をそれぞれかけて求めることができたので、同じように考えてみよう。 4÷2 9÷3 4 ÷ 2 9 ÷ 3 = 2 3 2 3 分数÷分数も同じように、分子同士と分母同士をそれぞれをわれば、できるね。 この方法は 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。




なぜ分数の割り算はひっくり返すのか お試し版




分数の割り算 Youtube
分数のわり算はひっくり返してかける理由 その1「分母を1にする」 を認めることを出発点とする考え方です。 ですが、分母の7/5を1にすることを考えます。 ですから、(1)の分母と分子に5/7をかけてみます。 ÷7/5 = /(7/5) =( ×5/7)/(7/5×5/7)分数のわり算の計算の仕方を、形 式的に理解し処理することは簡単であるが、「なぜ逆数にしてかけるのか」は 児童にとって理解が難しいと言われる。計 算の仕方を考える方法として、個人思考・集 団思考場面で取り上げたのは、[ わり算のきまりを根拠とした計算の仕方]と[数直線] を使った解決 割り算の基本 割り算は「 除法 」とも言い、 割り算の結果を 「 商 」と呼びます。 「 除 」には「 取り除く 」という意味があり、「 割り算 」とは「 いくつ取り除けるか 」という事です。 「 商 」は、むかし 商人 たちが「 自分たちの分け前や取り分を、はかる時 」に使っていたという説も




おもひでぽろぽろ 分数の割り算 かけ算にして上下逆にするのはなぜ Youtube




割り算を分数で表す問題 分数にするにはこれを覚えておけばok 中学や高校の数学の計算問題
6年算数 分数×分数 子どもの学習支援 by いっちに算数 スマホ版 フリー素材提供 分数×分数の計算の考え方をわかりやすくするために、このサイトでは、下のような算数アニメを用いています。 ※アニメの説明は記事中にありますので、ここでは参考にご覧下さい。無料でダウンロードして、何度でも印刷できます。 各学年向けの算数の計算問題プリントがあります。 問題と解答付きでダウンロードして印刷できます。 「毎回異なるプリントが作られます」をクリックして印刷してください。 印刷枚数を指定する 割り算「/」 これは、もともとタイプライターの時代に、分数を上下に打つことができなかったので、使われました。 パソコンになっても、 「÷」の記号はないので「/」を使います。 分数の「ー (横棒) 」を「ななめ」にしたと思ってください。




小学6年生 算数 無料問題集 帯分数 帯分数の約分の無い割り算 おかわりドリル



3
「1あたり」を求めるときはわり算! 分数÷分数はすごく難しいです! ですが、ポイントは 『1』のときいくらか? と聞く問題が多い、ということです。分数3つの項のわり算の問題を集めた学習プリントです。 分数には仮分数も含みます。 わり算の項を逆数にしてかけ算にして、途中式を立てます。 約分は複数回ある場合もあるので、もれなくしっかり探して答えを出しましょう。分数のかけ算 分数×分数(1) 問題一括 (3,354Kb) 解答一括 (3,775Kb) 分数×分数(2) 力をつけよう(1) 力をつけよう(2) 4 分数のわり算 分数÷分数(1) 問題一括 (3,3Kb) 解答一括 (4,621Kb) 分数÷分数(2) 乗除混合 文章問題 分数の倍とかけ算・わり算(1) 分数の倍とかけ算




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生




分数の割り算をする方法 12 ステップ 画像あり Wikihow
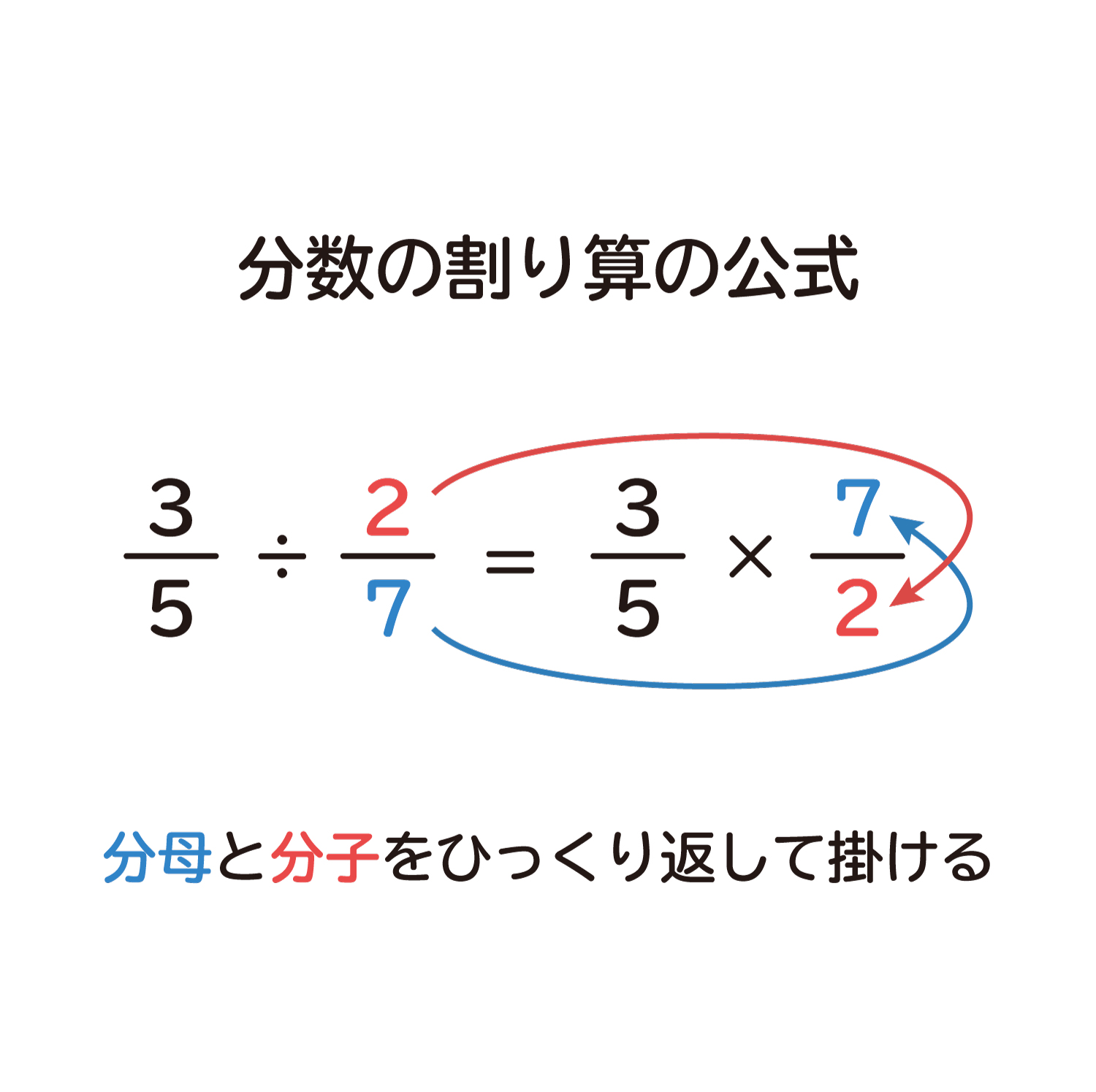
分数の割り算はひっくり返す! 分数の割り算は、たった一つの動作で掛け算に変身します。 割る数の分子と分母を逆にする これだけです! そうすれば、÷を×に変えることができます。 この分子と分母を逆にしたものを、「逆数」と呼んだりします。「分数のかけ算・わり算」の授業は,算数科で最も難しい授業になる。 どういう意味で難しいのか? 「分数のかけ算・わり算」の授業の難しさは, a 内容が,難解 b 推論の階梯が長い ではない。つぎのことから来る難しさである:わり算のきまり わられる数とわる数に同じ数をかけても答えはかわらない このきまりを思い出して、わる数の逆数を両方の数にかけるとわる数は1になります。 ※分数×分数の計算はすでに習っています。 結局、分数÷分数の計算は



割り算は2種類あるって知っていますか ー算数嫌いの子のための算数 I Learn Jp




分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話
「分数の割り算はひっくり返してかける」というのは、実は「唯一絶対の方法」ではありません。 ただ、 いろんな「分数の割り算」の場面を考え、その構造を一般化していった結果、「そうするとどんな"分数の割り算"でも同じように計算できる」というだけに過ぎない のです。割り算に直す方法 分数は割り算の省略記号なので,割り算に直すことができ,「ひっくり返して掛ける」と,掛け算になります. 分母を払う方法 もとの分数が普通の分数でない原因を考えると,7と3は犯人ではありません.3分の7というのは普通の分数です.分数(有理数)の指数が付いている式は累乗根で表される式と同じものです.多くの場合,分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります. 分数(有理数)の指数の定義 a>0 であって m, n が正の整数であるとき a mnn = n√




初等代数 分数を教える 通分 約分 足し算 大人が学び直す数学
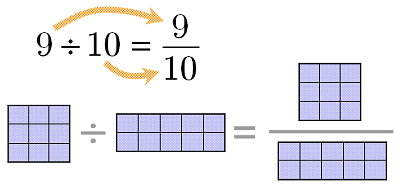



初等代数 分数を教える 割り算 大人が学び直す数学
定義 割られる数÷割る数 というものです。 また、分数は上の段と下の段に分かれていますよね。 上の段を「分子(ぶんし)」といい、下の段を「分母(ぶんぼ)」 といいます。 分子は割られる数で、分母は割る数 と同じ意味なのです。 ↓ つまり、割り算と分数の関係をイラストであらわすと、次のようになります。 割り算記号の左を分数の上の段に




余りがある分数の割り算 って難しいからわかりやすくした Soutai 40




分数の割り算 3 5 1 2 ビデオ 分数を分数で割る カーンアカデミー




分数のわり算2 Youtube
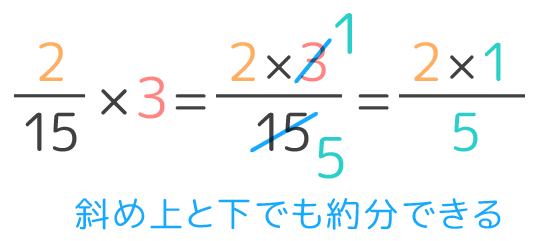



小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館




小学5年生向け分数のかけ算問題
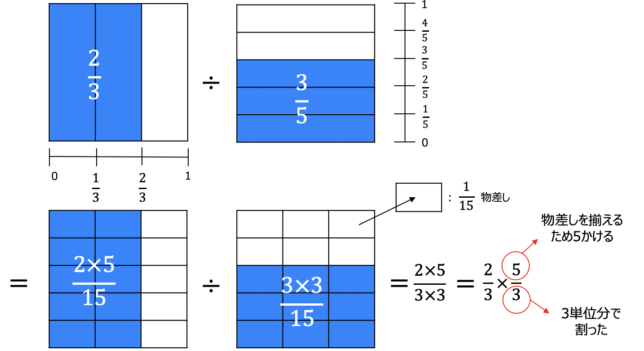



何で分数の割り算は逆数をかけるの 理由を説明できますか




分数の授業9時間目 分数の割り算 石原清貴の算数教育ブログ




6年生 分数の割り算 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




なぜ分数の割り算はひっくり返すのか Home Facebook




今さら聞けないシリーズ 分数の割り算はなぜ逆数にしてかけるのか 1で という発想がポイント マナビバ Com




数学塾直伝 分数の割り算の教え方と詳しい理屈 どうしてひっくり返すのかがよくわかる 永野裕之のblog




分数の割り算はなぜ分母分子を ひっくり返して掛け算 になる 理数系無料オンライン学習 Kori




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生
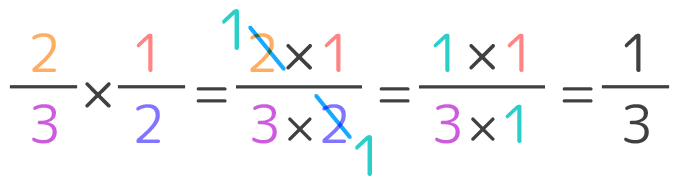



小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館




なぜ分数の割り算はひっくり返すのか 数学ギライの人のためのやり直し講座 ダ ヴィンチニュース




分数の割り算はなぜひっくり返してかけるのか その理由を解説 空間情報クラブ 株式会社インフォマティクス




分数の割り算の計算プリント 帯分数編 全180問無料 算数パラダイス




分数 分数 の割り算 計算ドリル 問題集 数学fun




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ



なぜ 分数の割り算は分母と分子をひっくり返して掛ける のか を説明します おかわりドリル




帯分数 帯分数 の割り算 計算ドリル 問題集 数学fun




中1数学 正負の数 分数計算のやり方を問題解説 数スタ
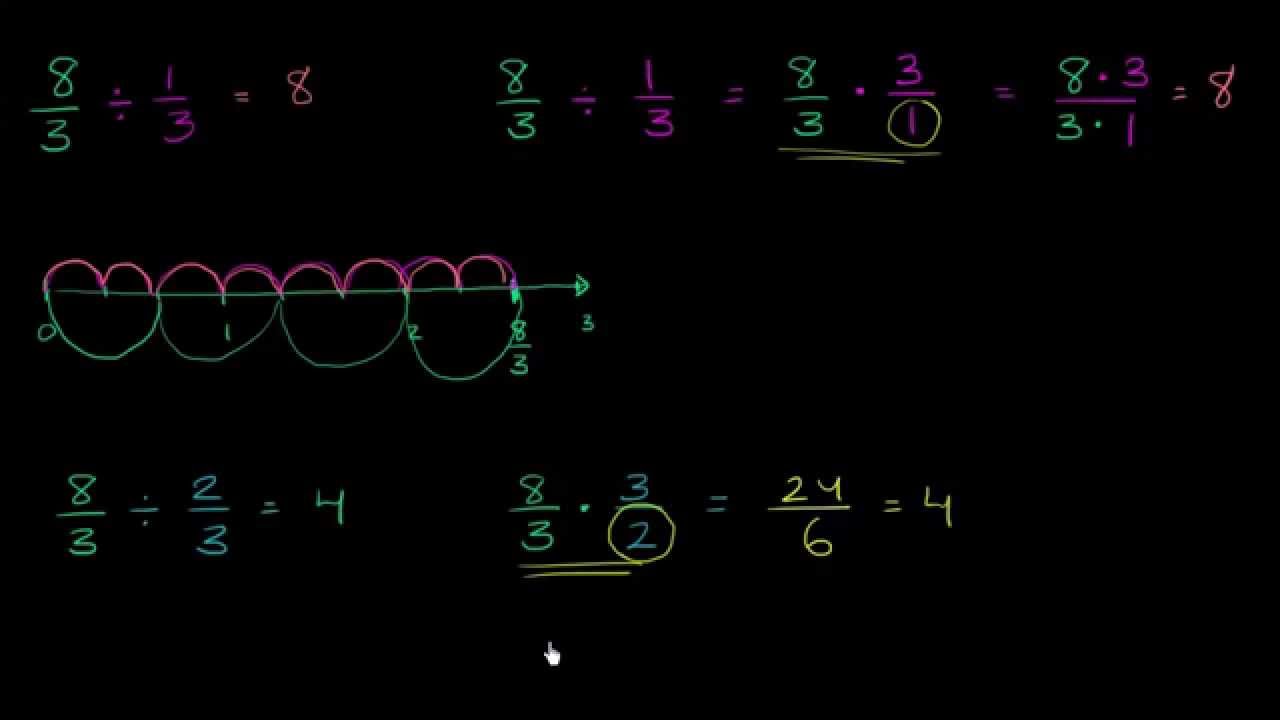



分数どうしの割り算を理解する ビデオ 分数を分数で割る カーンアカデミー




Make A Wish 分数の割り算




分数の割り算は割り算の分数 1ncrement
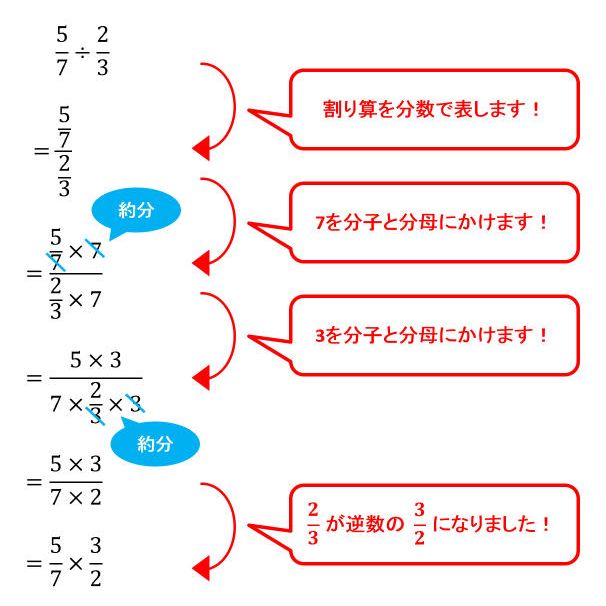



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料



分数のわり算 小6 タイル図での指導
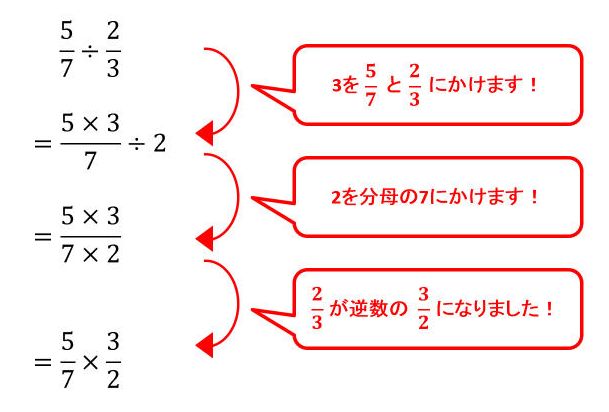



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
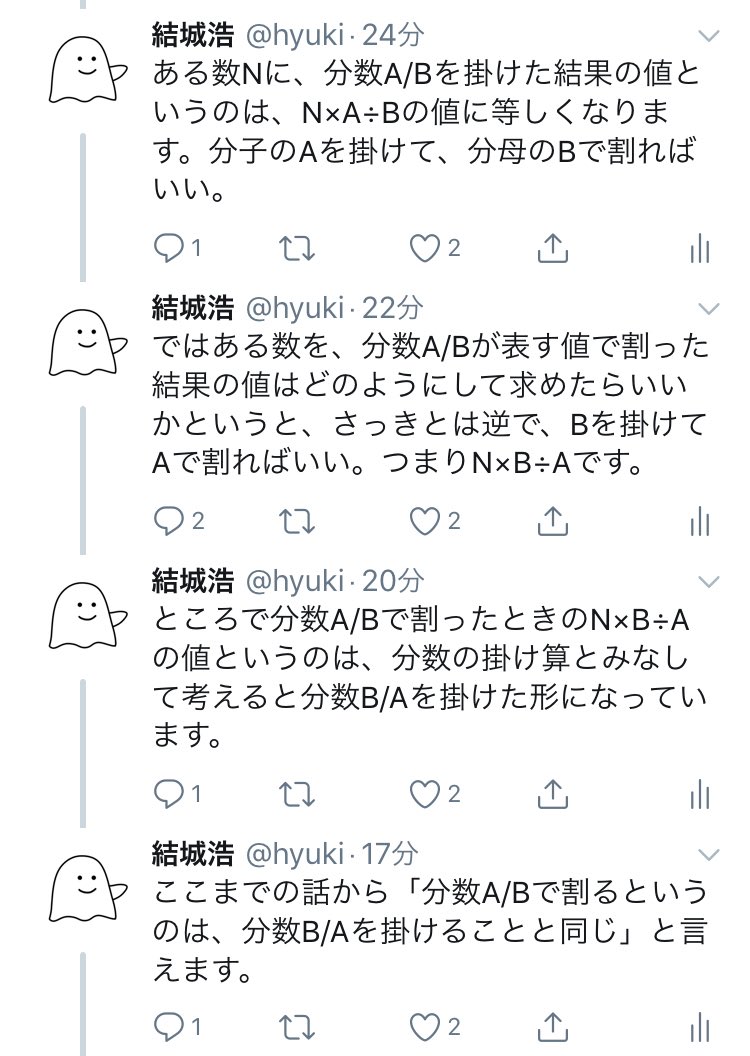



結城浩 添付画像をみてください 分数の割り算 を わからない 人はこの画像を読み飛ばします わかりにくそうだからです でも この四つのツイートには 分数の割り算を行うときに 分子と分母をひっくり返してうまくいく理由 が書かれています ですから




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




分数の割り算をするときに 逆数をかけるのはどうしてだろう おとなぱすた



分数のわり算2 分母どうし分子どうし割ってはいけないか




分数の割り算はなんで逆数を掛けるのか 横浜市東戸塚にある個別指導塾教室長のブログ




なぜ分数の割り算はひっくり返すのか お試し版 中学 勉強 分数 割り算



6年算数分数 分数 分数のわり算 教え方



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




整数と分数の割り算について 整数と分数の割り算について教えてくださ 小学校 教えて Goo



分数のかけ算 わり算2 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




Amazon Fr 新版 なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる Livres



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料



1




小学生向け 算数 プリント 分数同士のかけ算 割り算テスト 学習塾 Step By Step
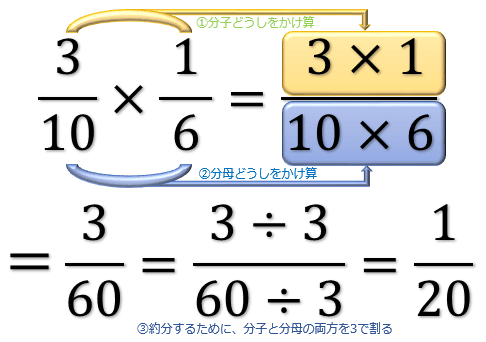



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
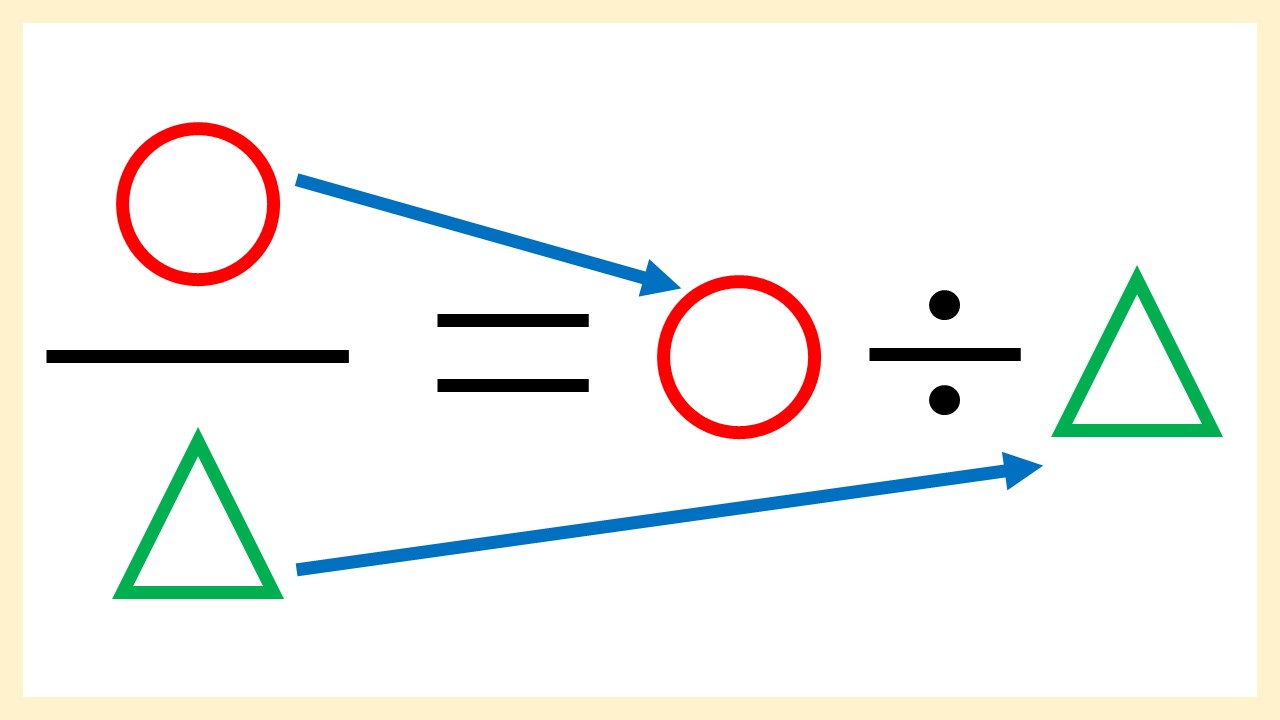



よくわかる 分数を割り算に直す方法 例題あり



分数の割り算に通分を使う トトロのパソコン珍道中
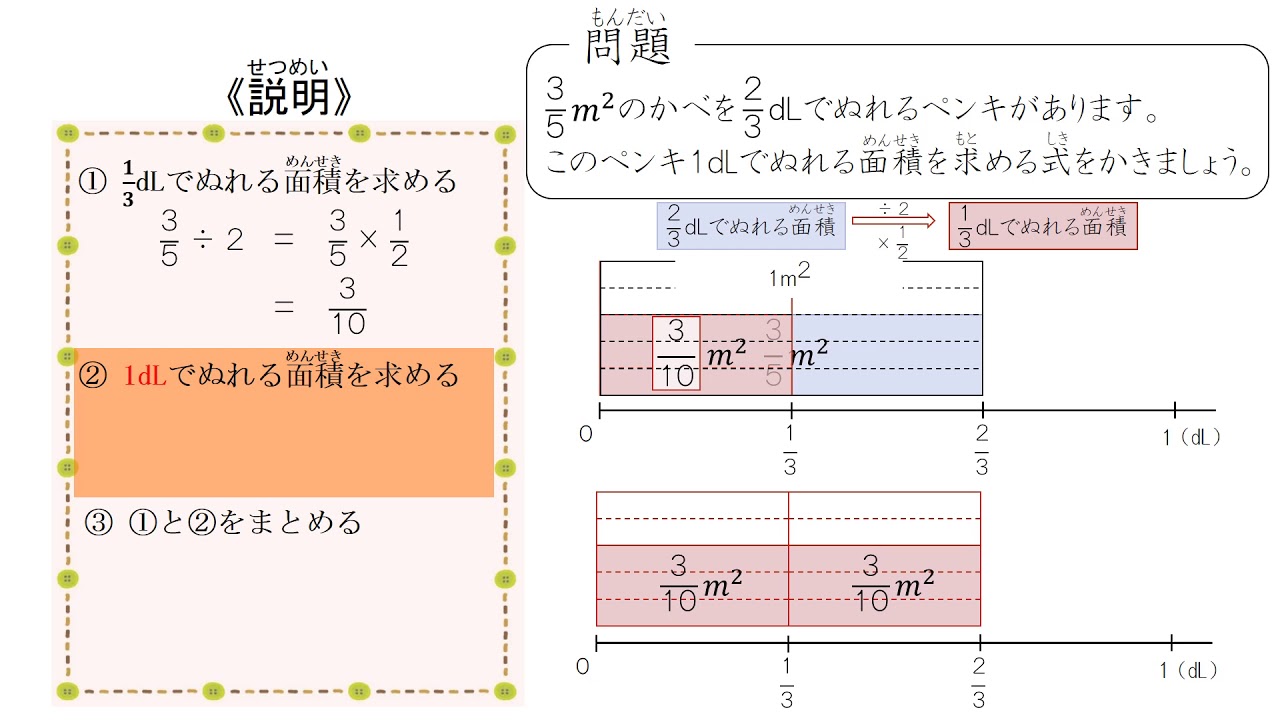



小6 分数のわり算 概念 面積図 日本語版 Youtube



ピザで理解する分数の割り算の意味 Qiita



しょうちゃん 公式ブログ 算数の問題を解いてみる その86 分数の割り算 Powered By Line




号外 やまねこ新聞社 わかりやすい分数の割り算
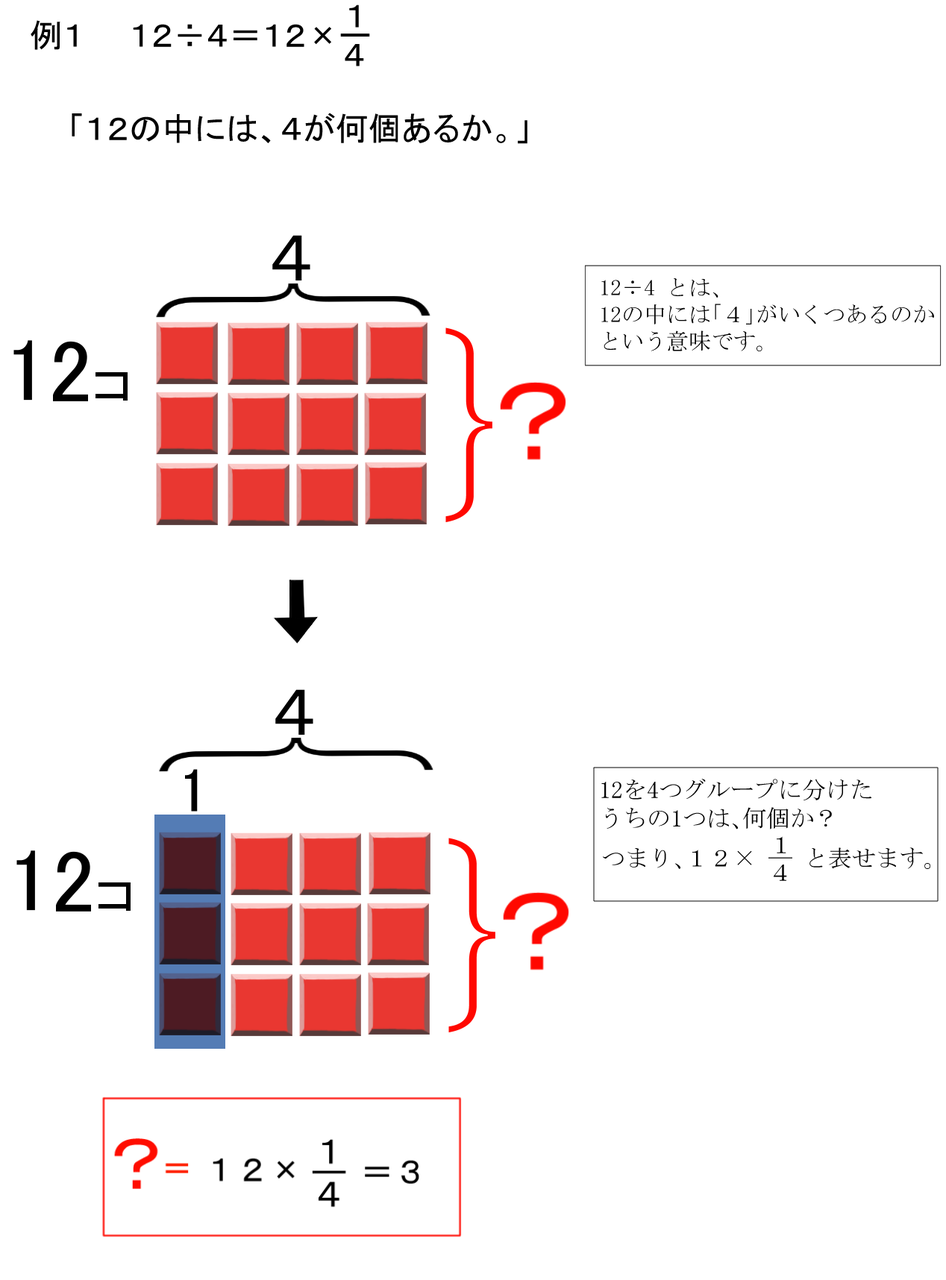



疑問1 なぜ分数の割り算では 分子と分母を逆にするの バカでもわかる 中学数学
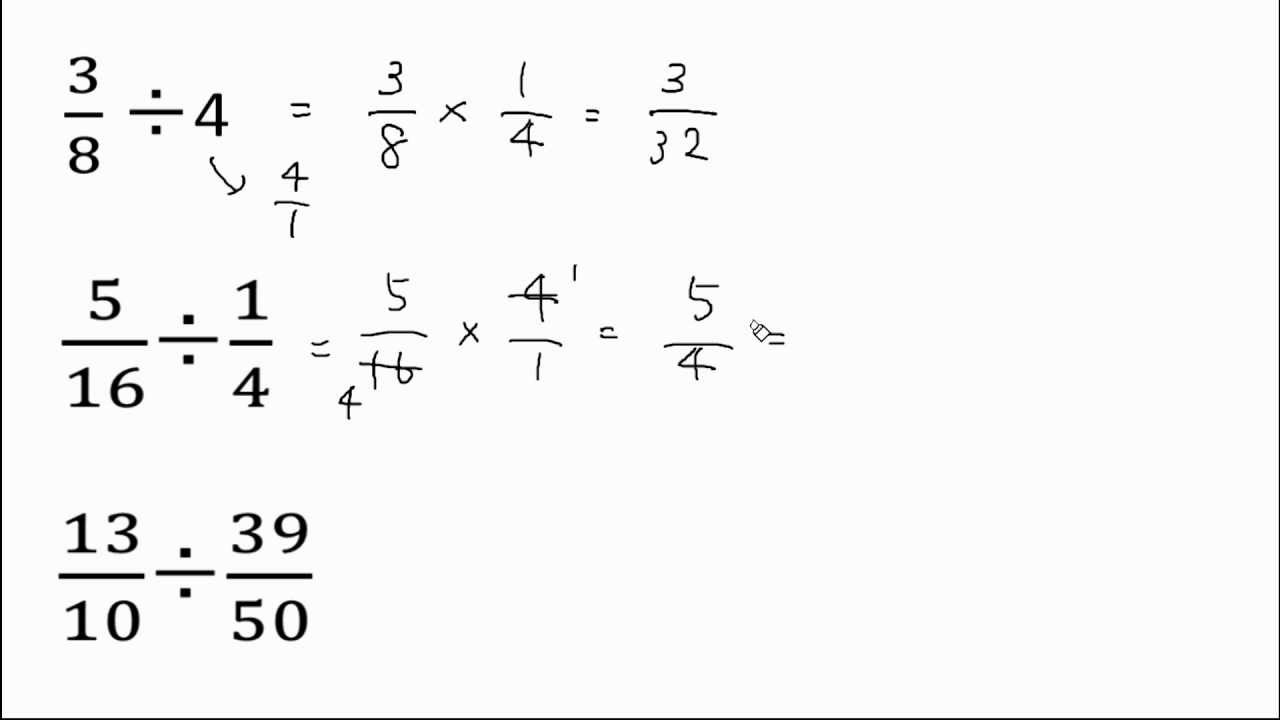



分数のわり算 問題練習 Youtube
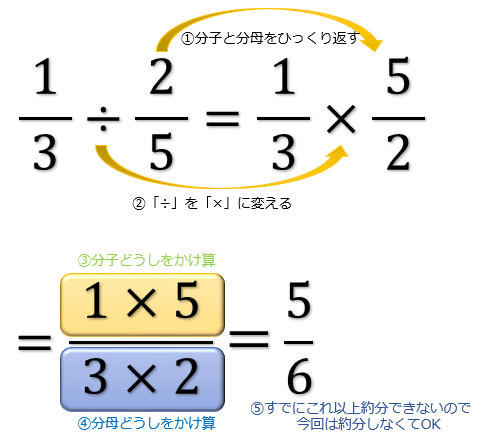



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




分数の割り算の計算プリント 真分数編 全240問無料 算数パラダイス
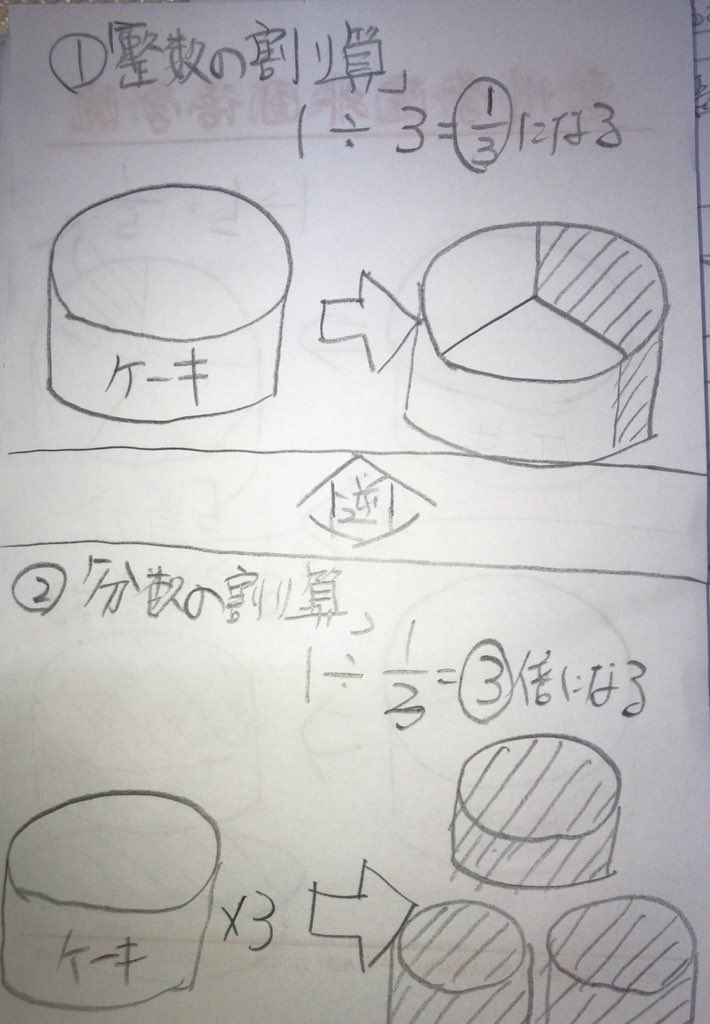



分数の割り算




6年生算数ドリル 分数 分数のわり算
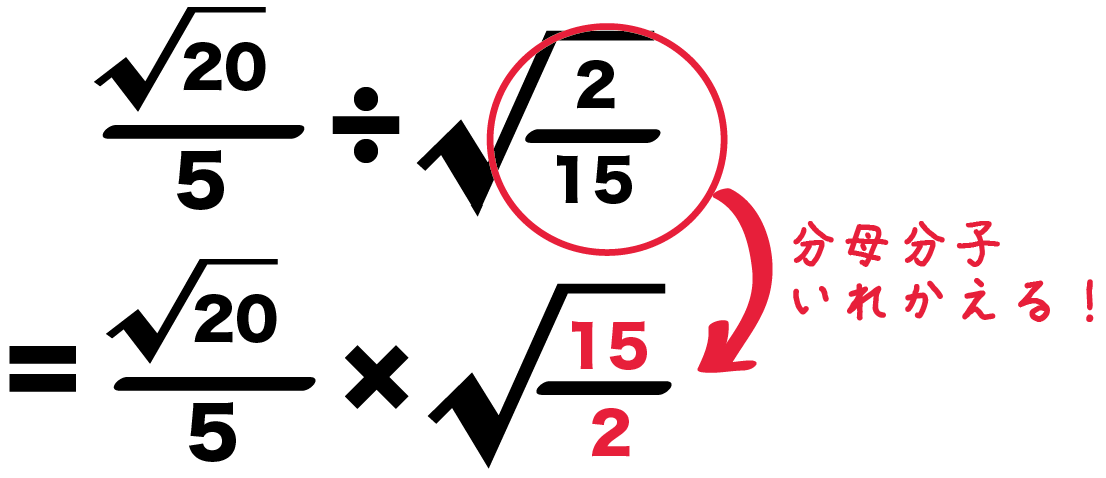



平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
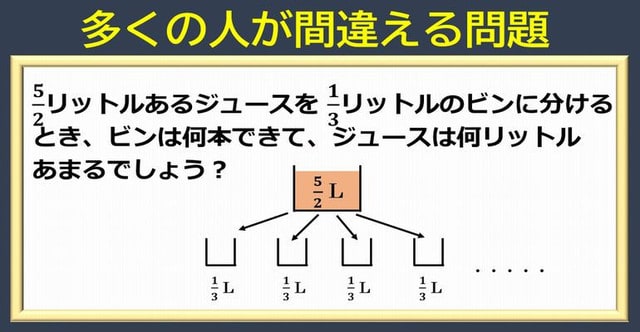



算数クイズ 間違える人が続出 冷静に解きたい分数の割り算の面白い問題 暇つぶしに動画で脳トレ




分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話
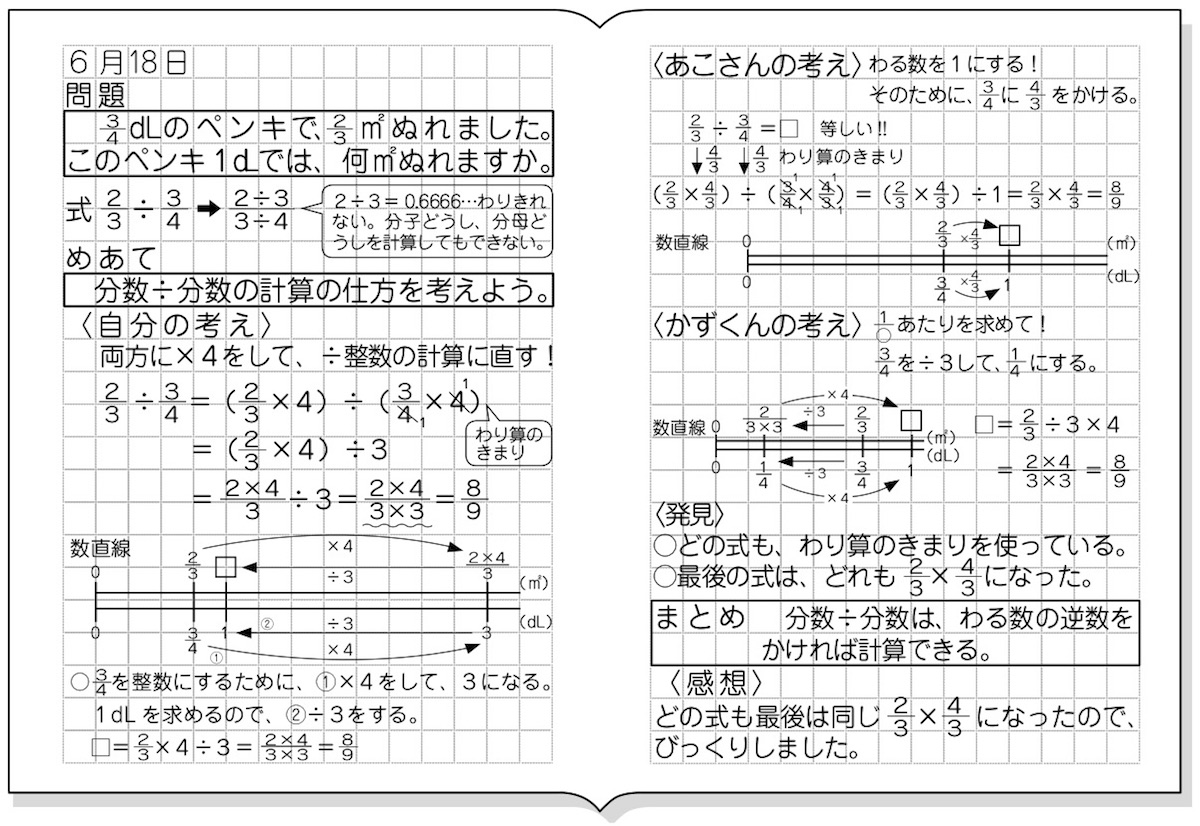



小6算数 分数のわり算 指導アイデア みんなの教育技術



分数の割り算をどう学ぶか 解答募集 Raising Kids With English Is So Much Fun 楽天ブログ



1



なぜ分数の割り算はひっくり返すのか 板橋 悟 バーゲン本 バーゲンブック Buyee Buyee 提供一站式最全面最專業現地yahoo Japan拍賣代bid代拍代購服務 Bot Online




6年生算数ドリル 分数 分数のわり算




分数の割り算の問題 やり方は逆数をとってかけるだけ 中学や高校の数学の計算問題




分数の割り算を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




割ると1あたり量がでる かけ算わり算の本来の意味を活用して文章題を克服する こどもの居場所 Inoこども塾
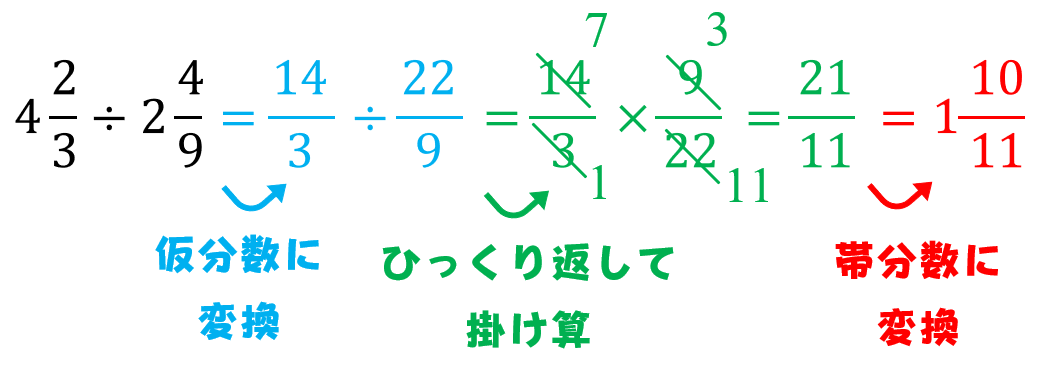



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




分数から割り算にする方法 迷ったらこのように覚えると楽 中学や高校の数学の計算問題
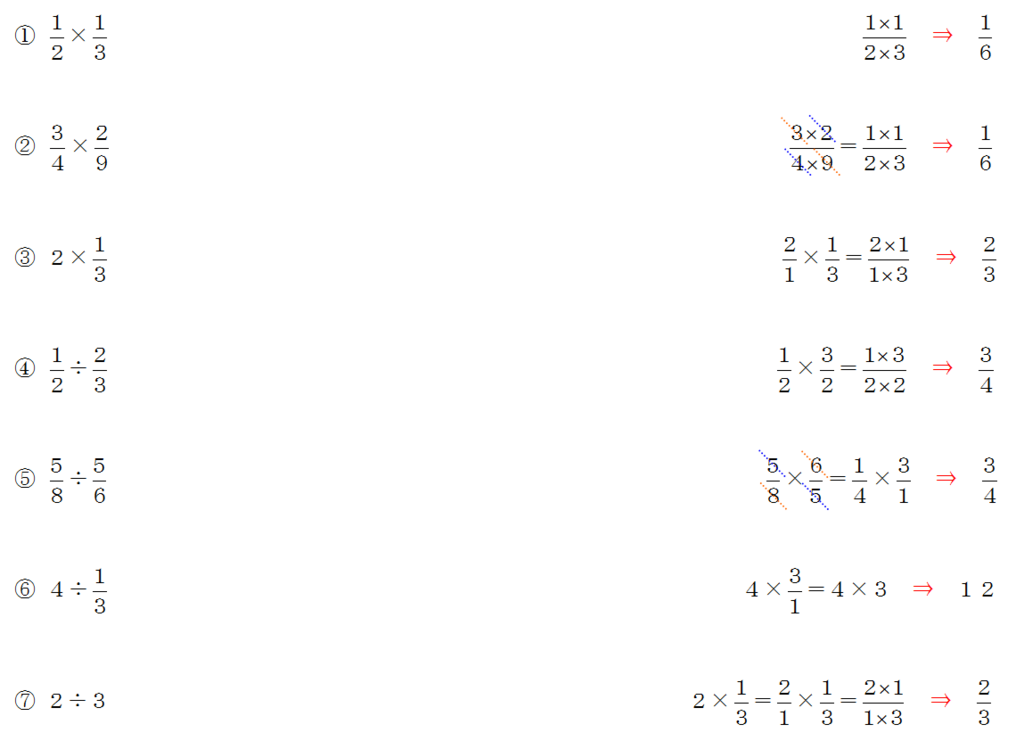



分数の掛け算や割り算の問題 計算のやり方は簡単だ 中学や高校の数学の計算問題




分数の割り算 なぜひっくり返す 分母をそろえて 朝日新聞デジタル



分数の割り算はなぜ逆数をかけるのか オンライン講師ブログ



わり算2 オイラーに習う分数の割り算 大学への算数 Ena国際部




分数の割り算はなぜ逆数をかけるのか 小学生の子供に説明する方法 数学fun




分数の割り算はなぜひっくり返してかけるのか その理由を解説 空間情報クラブ 株式会社インフォマティクス




分数の割り算の計算プリント 真分数編 全240問無料 算数パラダイス




分数の割り算はなぜひっくり返してかけるのか 高校数学なんちな




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生




Amazon Fr なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる Livres




すきるまドリル 小学6年生 算数 分数のわり算 無料学習プリント すきるまドリル 無料学習プリント




小6 分数の割り算問題
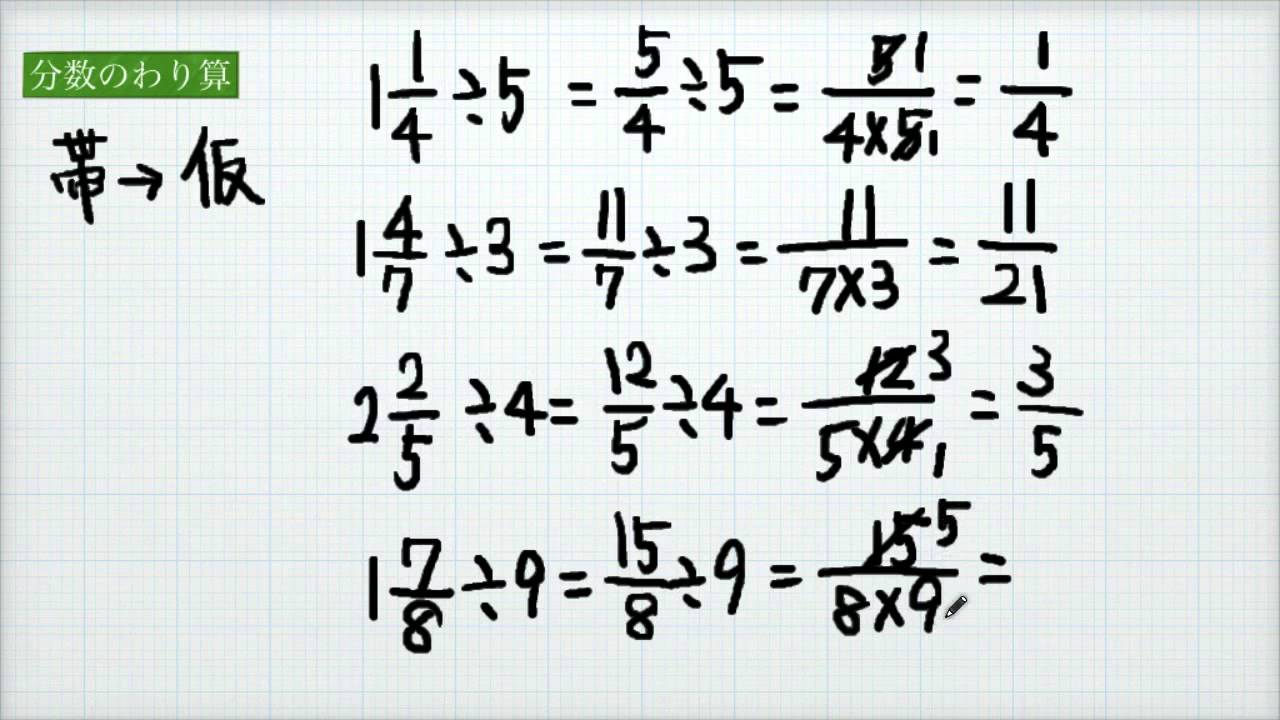



小学校5年 算数 分数のわり算3 帯分数のわり算 Youtube




分数の割り算の考え方と解き方 なぜ割る数を逆数にしてかけるか Cocoiro ココイロ Part 3




小学6年生の算数 帯分数と分数のわり算 練習問題プリント ちびむすドリル 小学生




分数の割り算の世界初の説明方法 アメリカの特許審査官殿に捧ぐ World S First Explanation Method Of Division Calculation Of Fractions 小僧の裏紙ブログ 楽天ブログ




小学6年生 算数問題プリント



分数の割り算 やり方の考え方と教え方




小学生向け 算数 プリント 分数同士の割り算 学習塾 Step By Step



0 件のコメント:
コメントを投稿