(1) で示した等式は「ヘロンの公式」(Heron's formula)と呼ばれる $3$ 辺の長さと面積が整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼び, そのうち $3$ 辺の長さが連続する整数であるものを「ブラーマグプタの三角形」(Brahmagupta triangle)と呼ぶこのページでは、 数学Ⅰの「三角比の公式」をまとめました。 三角比の公式と覚え方を、わかりやすく解説していきます。 数Ⅱの三角関数は「三角関数 公式一覧」で詳しく説明しているので、チェックしてみてください。 問題集を解く際の参考にしてください! このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比(\\(\\sin, \\cos, \\tan\\))を使った三角形の面積を求める方法はいくつ

任意三角形面积公式是什么
三角比 面積公式 証明
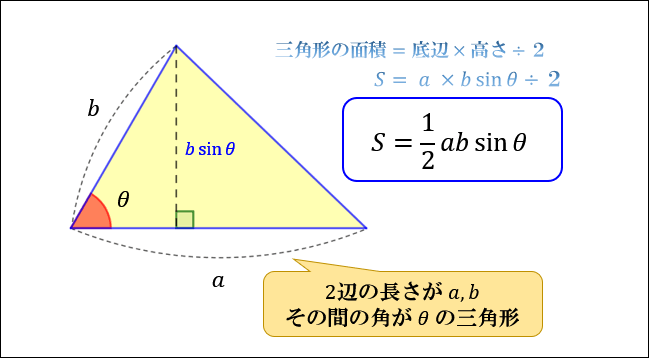
三角比 面積公式 証明-相似比k l のとき,表面積比はk l2 2 ,体積比はk l3 3 例題02体積がV の正四面体の各面の重心を頂点とする正四面体の体積をV を用いて表せ。 三角形の面積公式リスト 図のようにh, をとると 三角形の面積S は ① 1 S a h 2 = ← 1 2 ×底辺×高さ ② sin 1 S a b 2 = θすべての三角形について、 ・ 面積= (1/2)×「ある辺の長さ」×「別の辺の長さ」×「その間の角の sin」 によって求まる




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦
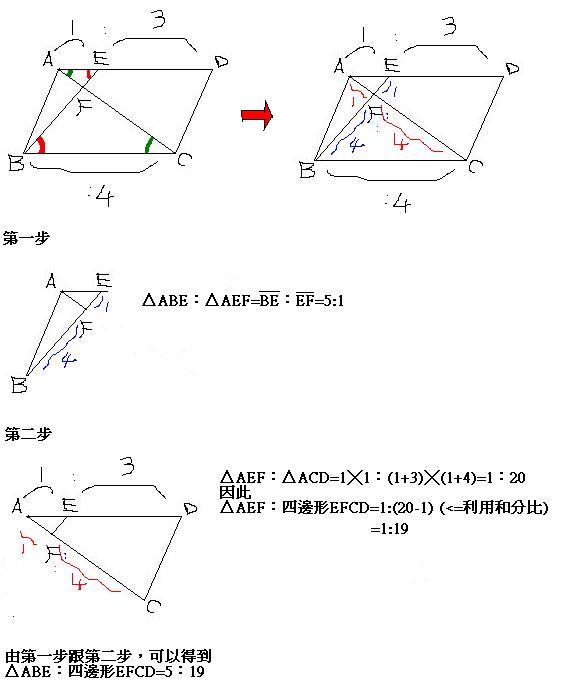
面積比の公式3選とは三角形 さて、今までの話を踏まえ、ここからは「 相似じゃない図形の面積比 」について考えていきます。 具体的には 高さが等しい三角形;三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。1角共有の三角形の面積比 解説 次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。
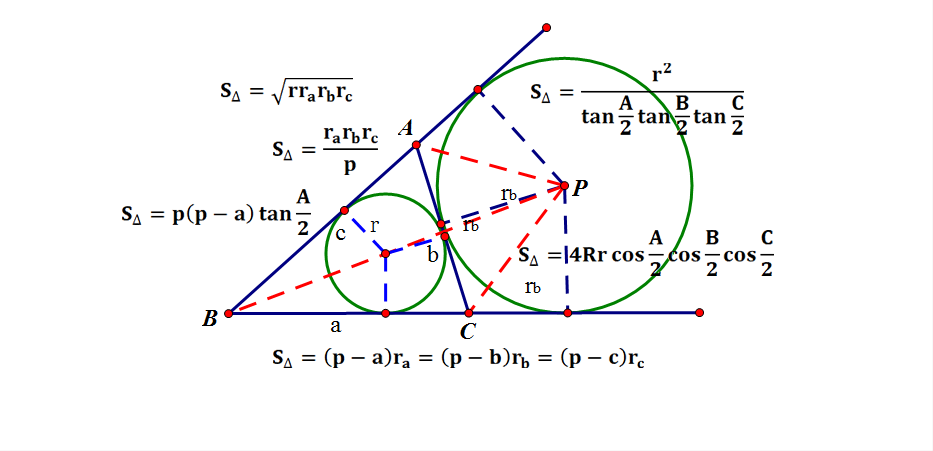
三角形の3辺の長さのみを用いて,直接三角比を用いないへロンの公式を導きます。 三角比を使った三角形の面積の公式は, 三角比の関係から, なので, ここで, より なので, また, とおくと, 同様にして, , なので, (へロンの公式) このように第1節三角比では、直角三角形の鋭角を定めたときの2辺の比を三角比とし て導入する。さらにそれらの相互関係に触れる。その後、鈍角への拡張となる。 そこでは、座標平面上で三角比が再定義される。続いて、再定義された三角比 の相互関係が導かれる。2 三角比の定義についての検討 2 l標準的な三角比の定義 三角比の定義での角aは,はじめ直角三角形 について考えるため,鋭角,つぎに鈍角へと進 む。鋭角の場合は座標系を用いないで,直角三 角形の辺の比として三角比を定義するほうが
13 三角形の面積の公式あれこれ 単元等 数学Ⅰ 図形の計量(三角比) Contents ・面積の公式の証明 ・面積の公式で遊ぶ 1 授業の内容 (1) 三角形の面積の公式を証明する (2) 公式を利用して三角形の面積を求める (3) 面積を利用して線分の長さを求める三角比基礎 >> 三角比(trigonometric ratio)是三角學(Trigonometry)的基本概念之一。簡單嚟講係指一個直角三角形入面兩條邊嘅比。喺初中階段,三角比嘅只會適用及出現於直角三角形上。 在定義三角比函數sin, cos及tan 時,我地要先知道咩係斜邊、鄰邊及對邊。頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b



三角函数公式 快懂百科




高校数学 3辺 三角形の面積 を求める方法 映像授業のtry It トライイット
三角比を利用して三角形の面積を求めるときには,まず図をかいて,どこの辺や角がわかっているかを確認します。 そして, の公式を使うために,必要な 辺 , 辺 , 角 でわかっていないものは何かを調べ,その「準備」をします。 あくまで三角形の面積の公式は $$(底辺)\times (高さ) \times \frac{1}{2}$$ でありますし、これに対して異論は無いはずです。なので私たちはこれからこの公式を「三角比が出てくる形」に変えてあげることを考えます。では早速やってみましょう。在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR 2 ,所以圆心角为n°的扇形面积: 比如:半径为1cm的圆,那么所对圆心角为135°的扇形的周长: C=2RnπR÷180=2×1135×314×1÷180==4355 (cm)=4355 (mm)




扇形面積公式 公式 推導過程 注意事項 中文百科全書




Cs9u0hft1yh 7m
やっぱり、敷地の面積を求めていたのか!ただ、三角形の辺の長さを測るだけで面積が求められるの? 「ヘロンの公式を使えばいいんです」。 ヘロンの公式が使われていた 図3 三角形から生まれる美しい数のリズム「三角比」。 手始めに、高さが同じ三角形の面積比の求め方を考えましょう。 三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」でしたね。4/7 三角比を使った三角形の面積の公式(6分15秒) 5/7 三角比を使ってケーキを等分に切る(3分24秒) 6/7 三角形を使って正多角形の面積を求める



三角形面积公式 直角等腰三角形面积公式 站长之家 查询网




三角形画像 三角形画像加工アプリ Christinecocajp
しかし、裏ワザ公式に頼ってしまうと 応用問題が出されたときに 対応しきれない部分もあるので できるだけ、比を辿っていく方法で覚えておいて欲しいです。 裏ワザ公式は、答えがあっているかの確認などで 利用してもらえれば効果バツグンなはず



三角形的面积公式二叙 知乎




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



高中必背三角函数公式大全有哪些公式 公式大全 壹壹高考网




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




三角形の面積の三角比を用いた公式 数学の偏差値を上げて合格を目指す




三角函數 三角形面積公式 Youtube




高中數學三角函數公式匯總 沒有比這更全的了 趕緊拿回去 趣讀



三角函数 玄数




れん 公務員 V Twitter 数的処理の図形問題でこの面積の公式知ってるとめっちゃ便利です 裏ワザみたいなもので 引っ掛けとか関係なく解けてしまいます これに加えて余弦定理と三角比の相互関係知ってると図形問題はほとんど片付きます



例題 三角函數 三角形面積公式 Iii 平面坐標與向量 高中的數學 Math Pro 數學補給站



考生必记 三角函数公式汇总 记忆 没有比这更全 知乎




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫



數學 高二上三角函數公式 小編過路君子



三角函数面积公式大全 初三网




高二高中數學的三角函數公式整理筆記 Clear




玩轉兩弦定理 看如何解三角形 每日頭條




三角形面積秒殺法 有實力的你也值得擁有 就是快 每日頭條




Sin Cos Tan公式sin Yzkgo




高校数 三角比 三角形の面積 3辺の長さから オンライン無料塾 ターンナップ Youtube




三角形の面積 三角比 Geogebra



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




三角形面積公式 兩邊一夾角 Youtube



數學 高二上三角函數公式 小編過路君子




数学 三角比 三角形の面積 公式 オンライン無料塾 ターンナップ




3 10 三角形面積公式的推導 Youtube




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积



余弦定理求三角形面积公式 高考辅导网



圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊




任意三角形面积公式是什么




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear
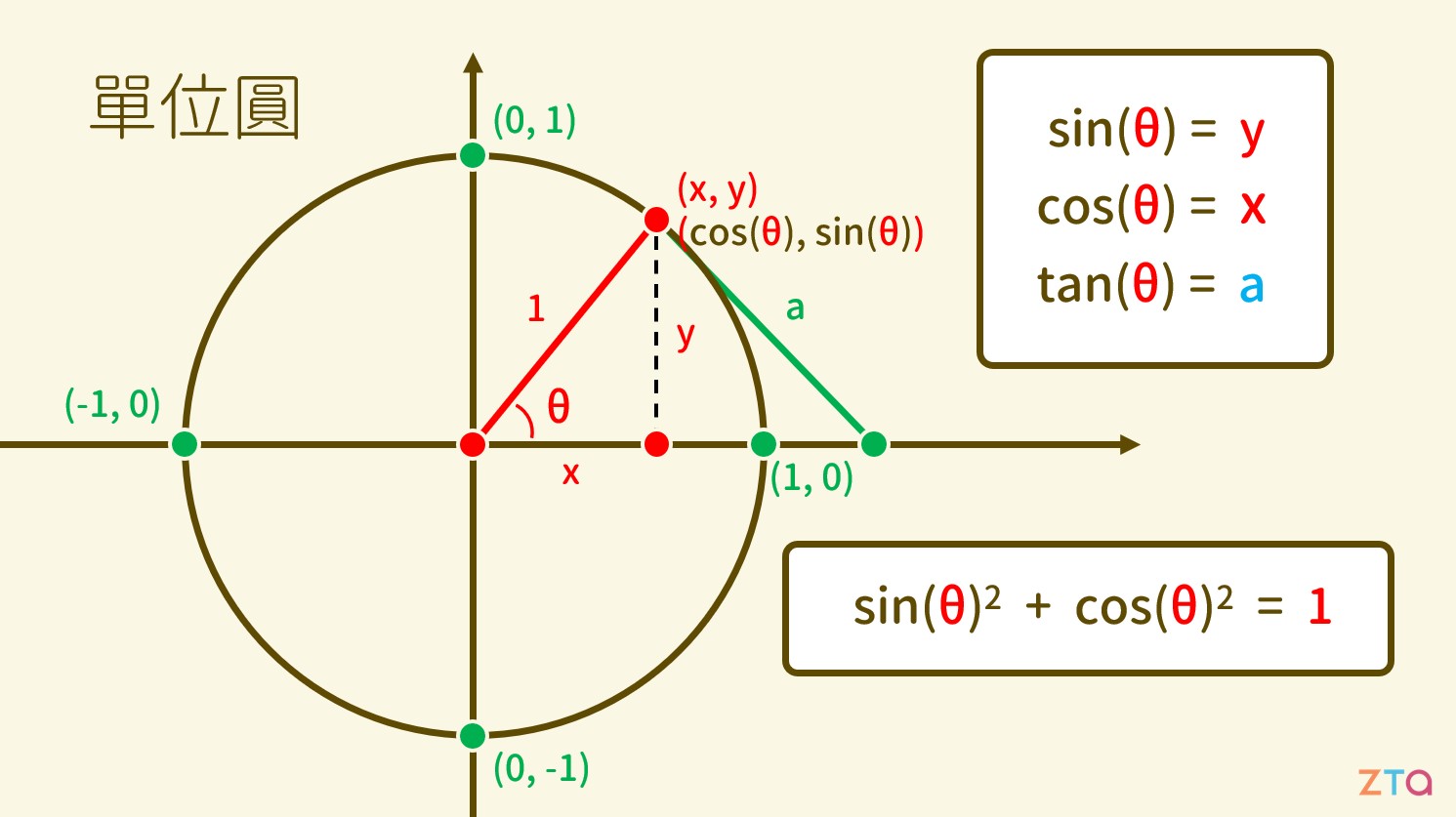



三角函數公式整理 學呀 基礎數學 數學 Sin Cos Tan 單位圓




弧長公式三角函數三角函數 Thomblake



數學 高二上三角函數公式 小編過路君子




單元12 三角比的性質



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




一道面積比公式的另證 的回響 用三角形的a S A 面積公式




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月



余弦定理求三角形面积公式 高中数学



Blog Archives 我的m讚




2 3正弦餘弦定理



1




三角函数 维基百科 自由的百科全书



高中必背三角函数公式大全有哪些公式 公式大全 壹壹高考网



1
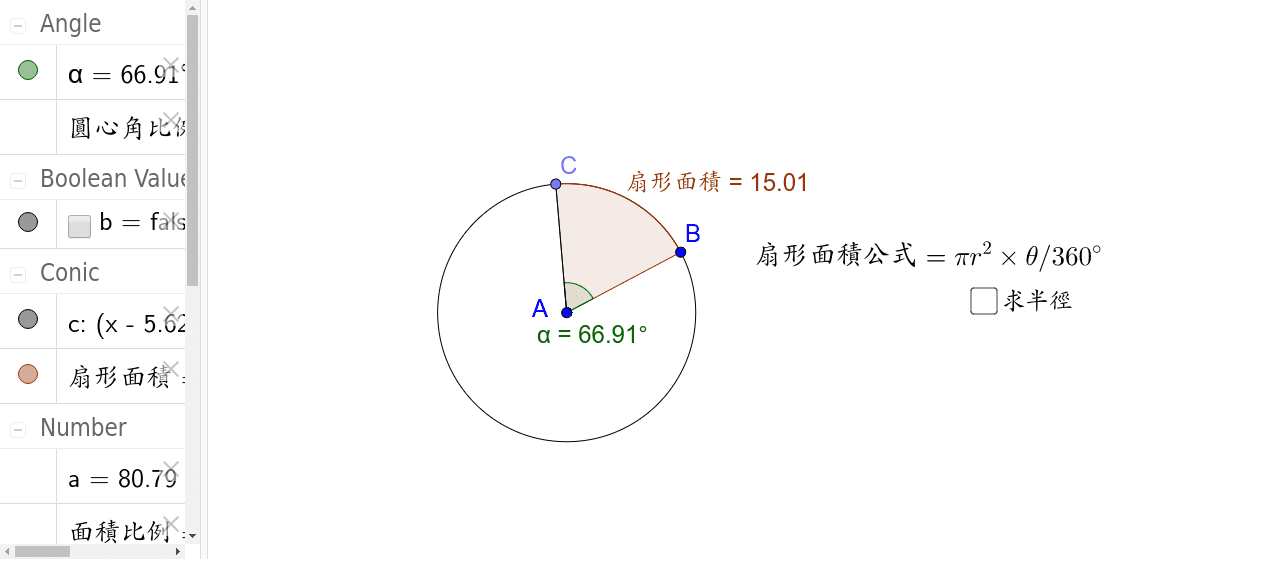



扇形面積公式2 Geogebra




三角比1 3面積公式與正餘弦定理習作這題怎麼算 Clear



扇形面積計算公式第二章三角函數 rbmi




三角函数正弦定理和余弦定理
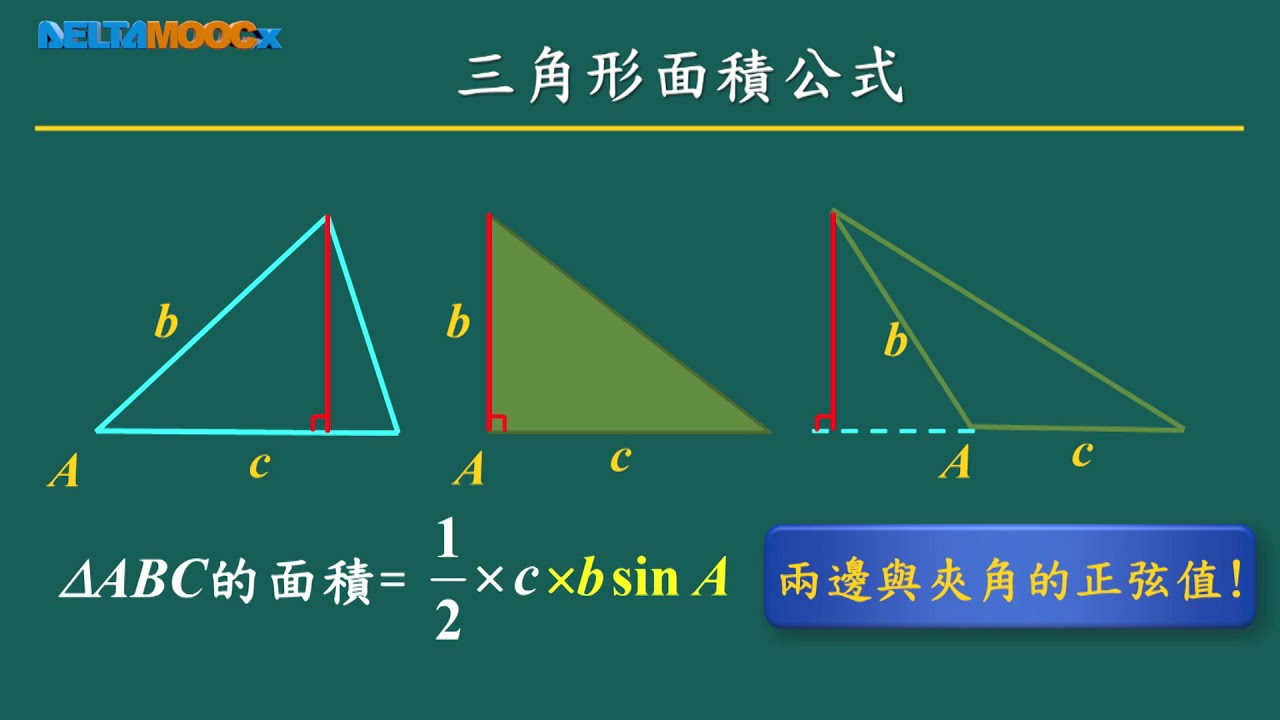



高中數學 三角函數 正弦定理與餘弦定理 1 三角形面積公式 吳汀菱 Youtube




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




三角形面積公式sin 三角形面積公式 Duph




三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア




数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ




数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ
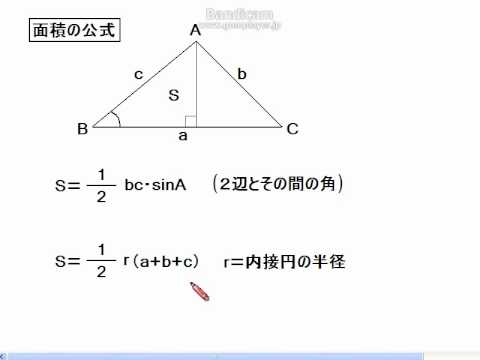



いちちの数学 三角比 面積の公式 Youtube




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积
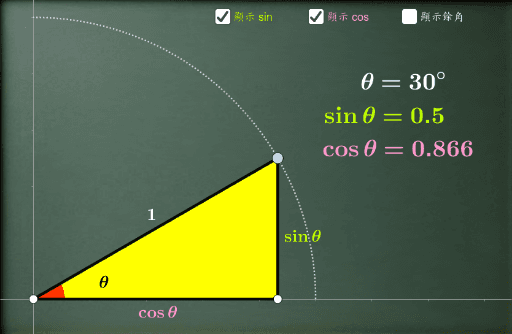



三角 Geogebra
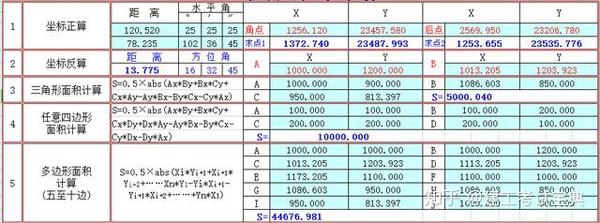



Excel函数公式大全 直接套用 计算速度计算器都比不上 快收藏 面积函数表格 双偶网
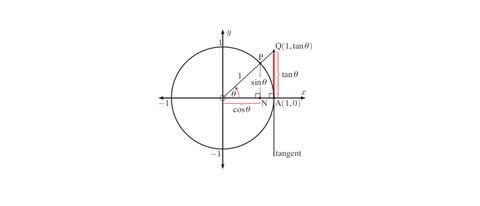



数 你好看 任意角三角函数与诱导公式 知乎



三角函数公式 快懂百科




三角形面积是平行四边形面积的一半对不对




高中數學 三角函數 數乙 弧長與扇形面積公式i 曾政清 Youtube
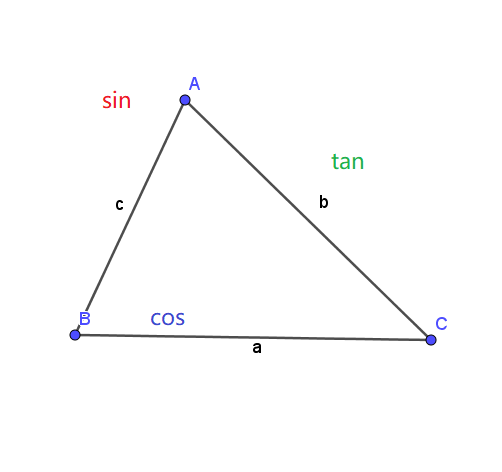



三角形中三角比的特殊公式 知乎




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear



數學 高二上三角函數公式 小編過路君子




扇形面积公式弧度制极坐标三种3个推导过程 计算机器在线计算



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊




如何快速記憶高中繁雜的數學公式之三 特殊的三角函數值記憶




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




三角比公式整理




解三角形知识点归纳 附三角函数公式 Docx 三九文库网




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦



Q Tbn And9gcq Hqeajhkitlcwnwlppuyepcnpxetx5choj5msbtvfox8yjkaz Usqp Cau



Http Www Takwing Idv Hk Dse Room Dse Maths Teaching Core Dse 13 Trigo 3 Pdf



三角形 玄数



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻
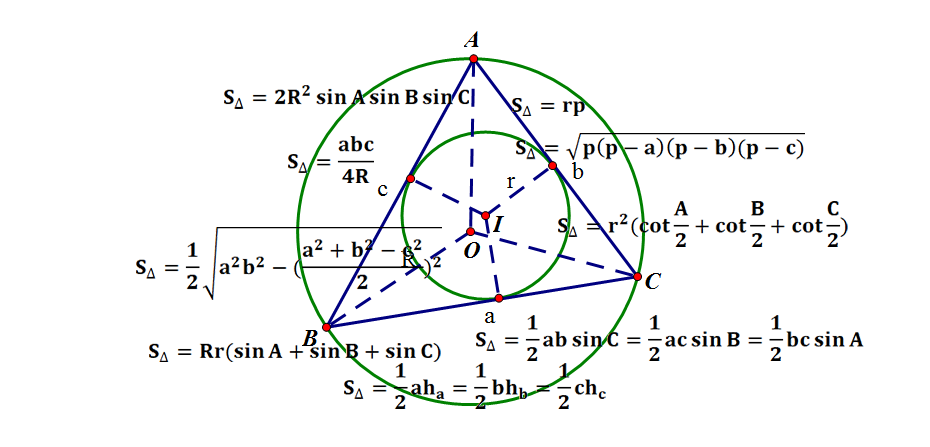



从三角形的面积公式谈起 知乎




高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube




三角形的面积公式小学




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角形正弦面积公式 搜索结果 哔哩哔哩 Bilibili



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积



Q Tbn And9gcr49hxcfjd6hwbvovxncwngpccdui3oq92zteqdpcwimlm8aj P Usqp Cau




正弦定理與面積公式的應用 重點精析 疑難點撥 第2講 每日頭條



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




高二高中數學的數學 三角函數 3 筆記 Clear




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




高中數學知識點總結 三角函數 解三角形 數列 導數總結 人人焦點




Sin Cos Tan公式sin Yzkgo




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
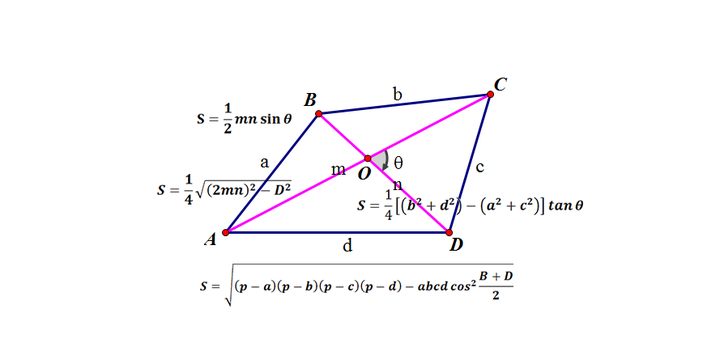



四边形的面积公式 知乎




三角函數的基本概念
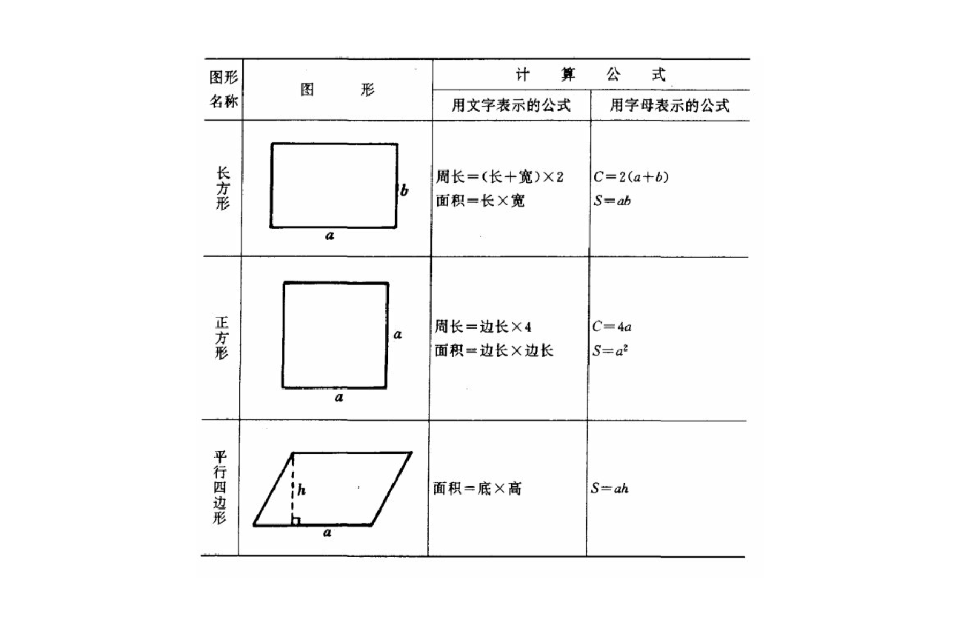



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



高中数学 三角形与三角函数最全知识点笔记总结 重难点



0 件のコメント:
コメントを投稿